Application of Derivatives to Nonlinear Programming for Prescriptive Analytics

• Data Analytics

Gone are the days when business analytics would bank on statistics alone. Besides the traditional probability theory and statistics, current machine learning techniques work in complete sync with linear algebra, graph theory, dynamic programming, multivariate calculus etc. As far as multivariate calculus is concerned, the different methods that lend support to machine learning algorithms are differential and integral calculus, partial derivatives, gradient and directional derivative, vector-valued function, Jacobian matrix and determinant, Hessian matrix, Laplacian and Lagrangian distributions etc. This blog will discuss the applications of second order derivatives and partial derivatives on optimization problems, as required for prescriptive analytics.

Prescriptive analytics provides precise decisions on the course of action necessary for future success. One of the prominent applications of prescriptive analytics in marketing is the optimization problem of marketing budget allocation. The business problem is to figure out the optimum quantity of budget that needs to be allocated from the total advertising budget to each of the advertising media like TV, press, internet video etc. for maximizing the revenue. The budget optimization problem is solved either through Linear or Nonlinear Programming (NLP) which depends on whether:

1. The objective function is linear/ nonlinear
2. The feasible region is determined by linear/nonlinear constraints

Thus, one of the important assumptions for linear programming is the constant returns to scale for each of the advertising media. However, in the real world, television advertisement data as plotted in Figure 1, defies such assumption as the graph shows a concave function. The constraint that may be considered for developing such optimization problem is the maximum amount that should be spent on a particular media and beyond that point any further expenditure may lead to the increase in revenue but at a decreasing rate. Thus, it’s important to find out the diminishing point of return for each of the advertising medium. Figure 1 has shown the revenue generated against the cost incurred for TV advertisement and both the cost and the revenue mentioned in the current paper  dollar value are in thousands.

Figure 1: Diminishing Point of Return for TV Advertisement

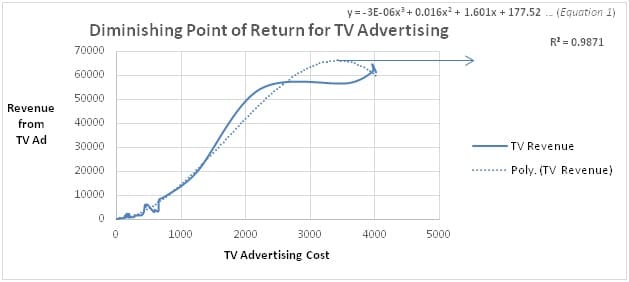
The curve that best fits the plotted revenue and cost of TV advertisement is cubic and is plotted in Figure 1 and mentioned in Equation 1. The R² achieved through the cubic equation is a whopping 98.7%. The first and second order derivatives of the cubic equation are calculated as follows:

The inflection point is identified where the second derivative changes from positive to negative. Therefore, mathematically, it’s the point where second derivative is 0, thus solving Equation 3, the cost at diminishing point of return is 1777.78 and the corresponding revenue at the diminishing point of return after plugging the value of x in Equation 1 is 36735.68. For further studies on the application of second derivatives on non-linear optimization, you may refer to Newton–Raphson algorithm and conjugate direction algorithms.

Partial derivative is the other prominent application of calculus on optimization problems. Partial derivatives is a function with several variables which are accomplished when a particular variable’s derivative is computed keeping other variables constant. One of the most widely used applications of partial derivative is the least square criterion where the objective is to find out the best fitting line by minimizing the distance of the line from the data points. This is achieved by setting first order partial derivatives of the intercepts and the slopes equal to zero. The other major applications of partial derivatives are as follows:

1. The second order partial derivative is used in an optimization problem to figure out whether a given critical point is a relative maximum, relative minimum, or a saddle point.
2. The assignment of penalty for conversion of an optimization problem to an unconstrained optimization problem through sequential unconstrained minimization technique.

The approaches discussed show how calculus can be integrated with nonlinear programming while delivering an optimized solution. In the same manner, Lagrangean-based techniques can also be integrated with Mixed Integer Non-Linear Programming (MINLP) to provide with the marketing budget optimization solution. Currently, data scientists cannot bank on a single technique to provide analytics solution. The real challenge is to figure out how multiple techniques can be creatively combined to provide a solution as unique as the business problem.